盘货东谈主类数学史上的三次危急, 临了一个危急于今仍旧无解!

数学，这门历史悠久的学科，不仅是科学探索的紧迫用具，更是东谈主类时髦特殊的基石。从古于今，数学的斟酌抑制鼓吹着科技的飞跃，但是，在这条发展谈路上，数学曾经面对过前所未有的挑战——三次紧要的数学危急。

这些危急并非意味着数学的倒退，而是科学探索历程中的必经之路。它们挑战了数学家们的想维极限，引发了数学表面的深刻变革，也转折促进了科学规模的赶紧发展。

第一次数学危急发生在公元前470年，源于毕达哥拉斯家数对荒唐数的发现。毕达哥拉斯是古希腊数学的伟大东谈主物，他的家数因阐发了勾股定理而申明远扬。

但是，方丈数成员希帕索斯发现等腰直角三角形的斜边无法用整数默示时，这个发现冲击了毕达哥拉斯的数学表面。毕达哥拉斯坚捏以为所罕有字齐不错默示为整数或整数之比，但希帕索斯的发现揭示了这一表面的局限。

面对这一悖论，毕达哥拉斯选拔了千里默和残酷，以致将希帕索斯千里入爱琴海，以真贵我方的巨擘和家数的正宗。尽管如斯，荒唐数的存在是不行否定的事实，这一数学危急直至1872年才由德国数学家感恩金通过有理数分割的表面得以贬责，荒唐数被阐述纳入数学体系，适度了长达2300多年的第一次数学危急。

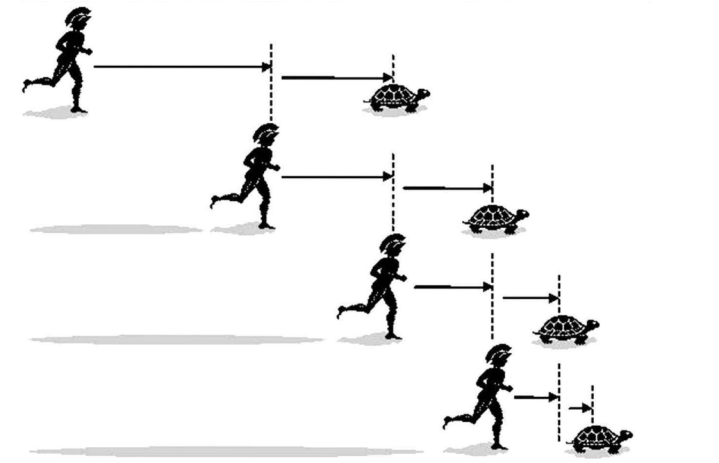
第二次数学危急发源于古希腊时间，与无限小的见解详细磋磨。芝诺建议的“芝诺的乌龟”悖论，以及中国旧书《庄子·六合篇》中刻画的“一尺之棰”，均响应了无限小和连络性的用功。这些悖论似乎标明，物体的带领和变化不错无限分割，从而引发了对无限小见解的准确性的质疑。

无限小是微积分表面的基石，若不贬责其界说问题，则微积分的表面基础即是不完备的。这获胜影响到牛顿力学体系等基于微积分的数学试验的正确性。

为了贬责这一危急，大批数学家投身于对无限小见解的斟酌，试图修补微积分表面的舛错。经过万古分的勉力，19世纪70年代，数学家威尔斯特拉斯、狄德金、康托等东谈主通过配置实数表面，最终贬责了第二次数学危急。

贬责无限小问题不仅完善了数学表面，还对数学、天文、物理等规模的发展产生了深刻影响。不错说，莫得第二次数学危急的挑战与贬责，当代社会的科技发展可能会滞后很多。

第三次数学危急发生于1897年，由数学家福尔蒂建议的剃头师悖论引发。这个悖论刻画了一位剃头师给我方定下端正：只给不给我方刮胡子的东谈主刮胡子。

那么问题来了，这位剃头师是否应该给我方刮胡子？这个看似罪恶的悖论本体上舒服了蚁合论的旨趣，而蚁合论依然成为数学的一大扶持。悖论的建议显现了蚁合论潜在的舛错，引发了对数学基础表面完备性的深刻质疑。

于今为止，第三次数学危急仍未获得透顶贬责。1931年，数学家哥德尔建议了不完备定律，阐发了数学本人在表面上的不完备性。这一定律不仅揭示了数学的局限，也标明了数学发展的永无尽头。天然这一危急尚未有定论，但它无疑鼓吹了数学表面的深入斟酌，也让咱们意识到，数学的探索之路远未走到尽头。

数学史上的三次危急，每一次齐对数学和科学界产生了深刻的影响。它们不仅挑战了其时的数学表面，促进了数学才略和想想的矫正，还催生了新的数学分支和科学表面。从荒唐数的发现到无限小见解的精准化，再到蚁合论的深入探讨，每一次危急齐明示着数学的无限可能性和科学的特殊。

这些危急告诉咱们，数学并不是一门完竣无瑕的学科，它的发展是充满挑战和争议的。但是，恰是这些挑战和争议鼓吹了数学斟酌的深入，使得数学成为了贬责科学问题、推脱手艺发展的宽敞用具。翌日，数学仍将不竭面对新的挑战，而每一次挑战齐可能是开启新常识大门的钥匙。